摘要:具体的数据预处理涉及重复值、异常值/缺失值/极端值、标准化和数据频率的处理。duplicated(subset=[key1,key2,duplicated(subset=[key1,key2,对数据范围内的所有因子做出如下调整:该方法不足在于,量化领域常用的数据如股票价格、token价格常呈现尖峰厚尾分布,并不符合正态分布的假设,在该情况下采用方法将有大量数据错误地被识别为异常值。...
前言
书接上回,我们发布了《用多因子策略构建强大的加密资产投资组合》系列文章的第一篇 - 理论基础篇,本篇是第二篇 - 数据预处理篇。
在计算因子数据前/后,以及测试单因子的有效性之前,都需要对相关数据进行处理。具体的数据预处理涉及重复值、异常值/缺失值/极端值、标准化和数据频率的处理。
一、重复值
数据相关定义:
- 键(Key):表示一个独一无二的索引。eg. 对于一份有全部token所有日期的数据,键是“token_id/contract_address - 日期”
- 值(Value):被键索引的对象就称之为“值”。
诊断重复值的首先需要理解数据“应当”是什么样子。通常数据的形式有:
- 时间序列数据(Time Series)。键是“时间”。eg.单个token5年的价格数据
- 横截面数据(Cross Section)。键是“个体”。eg.2023.11.01当日crypto市场所有token的价格数据
- 面板数据(Panel)。键是“个体-时间”的组合。eg.从2019.01.01-2023.11.01 四年所有token的价格数据。
原则:确定了数据的索引(键),就能知道数据应该在什么层面没有重复值。
检查方式:
- pd.DataFrame.duplicated(subset=[key1, key2, ...])
- 检查重复值的数量:pd.DataFrame.duplicated(subset=[key1, key2, ...]).sum
- 抽样看重复的样本:df[df.duplicated(subset=[...])].sample找到样本后,再用df.loc选出该索引对应的全部重复样本
- pd.merge(df1, df2, on=[key1, key2, ...], indicator=True, validate='1:1')
- 在横向合并的函数中,加入indicator参数,会生成_merge字段,对其使用dfm['_merge'].value_counts可以检查合并后不同来源的样本数量
- 加入validate参数,可以检验合并的数据集中索引是否如预期一般(1 to 1、1 to many或many to many,其中最后一种情况其实等于不需要验证)。如果与预期不符,合并过程会报错并中止执行。
二、异常值/缺失值/极端值
产生异常值的常见原因:
- 极端情况。比如token价格0.000001$或市值仅50万美元的token,随便变动一点,就会有数十倍的回报率。
- 数据特性。比如token价格数据从2020年1月1日开始下载,那么自然无法计算出2020年1月1日的回报率数据,因为没有前一日的收盘价。
- 数据错误。数据提供商难免会犯错,比如将12元每token记录成1.2元每token。
针对异常值和缺失值处理原则:
- 删除。对于无法合理更正或修正的异常值,可以考虑删除。
- 替换。通常用于对极端值的处理,比如缩尾(Winsorizing)或取对数(不常用)。
- 填充。对于缺失值也可以考虑以合理的方式填充,常见的方式包括均值(或移动平均)、插值(Interpolation)、填0df.fillna(0)、向前df.fillna('ffill')/向后填充df.fillna('bfill')等,要考虑填充所依赖的假设是否合。
- 机器学习慎用向后填充,有 Look-ahead bias 的风险
针对极端值的处理方法:
1.百分位法。
通过将顺序从小到大排列,将超过最小和最大比例的数据替换为临界的数据。对于历史数据较丰富的数据,该方法相对粗略,不太适用,强行删除固定比例的数据可能造成一定比例的损失。
2.3σ / 三倍标准差法
标准差 体现因子数据分布的离散程度,即波动性。利用 范围识别并替换数据集中的异常值,约有99.73% 的数据落入该范围。该方法适用前提:因子数据必须服从正态分布,即 。
其中,, ,因子值的合理范围是。
对数据范围内的所有因子做出如下调整:
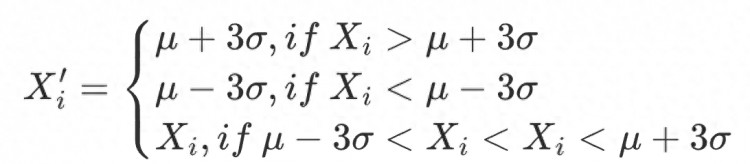
该方法不足在于,量化领域常用的数据如股票价格、token价格常呈现尖峰厚尾分布,并不符合正态分布的假设,在该情况下采用方法将有大量数据错误地被识别为异常值。
3.绝对值差中位数法(Median Absolute Deviation, MAD)
该方法基于中位数和绝对偏差,使处理后的数据对极端值或异常值没那么敏感。比基于均值和标准差的方法更稳健。
绝对偏差值的中位数
因子值的合理范围是。对数据范围内的所有因子做出如下调整:

三、标准化
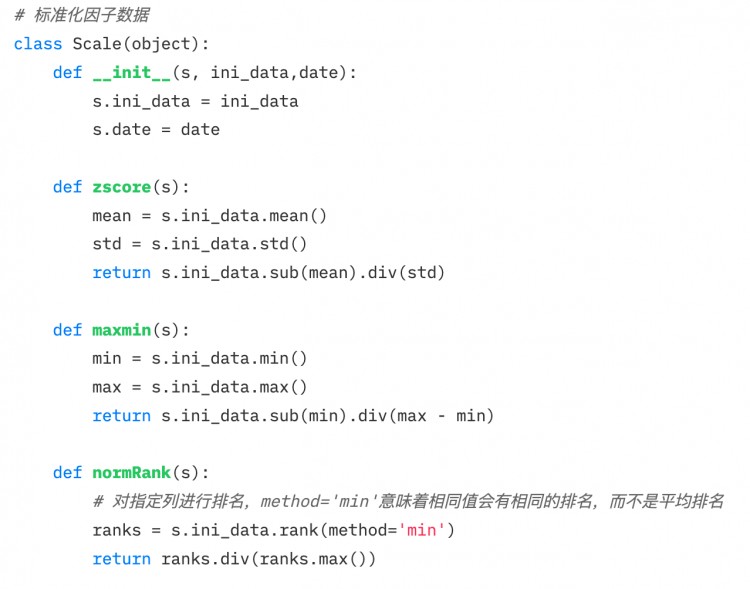
1.Z-score标准化
- 前提:
- 由于使用了标准差,该方法对于数据中的异常值较为敏感
2.最大最小值差标准化(Min-Max Scaling)
将每个因子数据转化为在 区间的数据,以便比较不同规模或范围的数据,但它并不改变数据内部的分布,也不会使总和变为1。
- 由于考虑极大极小值,对异常值敏感
- 统一量纲,利于比较不同维度的数据。
3.排序百分位(Rank Scaling)
将数据特征转换为它们的排名,并将这些排名转换为介于0和1之间的分数,通常是它们在数据集中的百分位数。*
- 由于排名不受异常值影响,该方法对异常值不敏感。
- 不保持数据中各点之间的绝对距离,而是转换为相对排名。
其中,, 为区间内数据点的总个数。
四、数据频率
有时获得的数据并非我们分析所需要的频率。比如分析的层次为月度,原始数据的频率为日度,此时就需要用到“下采样”,即聚合数据为月度。
下采样
指的是将一个集合里的数据聚合为一行数据,比如日度数据聚合为月度。此时需要考虑每个被聚合的指标的特性,通常的操作有:
- 第一个值/最后一个值
- 均值/中位数
- 标准差
上采样
指的是将一行数据的数据拆分为多行数据,比如年度数据用在月度分析上。这种情况一般就是简单重复即可,有时需要将年度数据按比例归集于各个月份。